Статистика

Математична статистика

Математична статистика — розділ математики та інформатики, в якому на основі дослідних даних вивчаються імовірнісні закономірності масових явищ. Основними задачами математичної статистики є статистична перевірка гіпотез, оцінка розподілу статистичних ймовірностей та його параметрів, вивчення статистичної залежності, визначення основних числових характеристик випадкових вибірок, якими є: вибіркове середнє, вибіркові дисперсії, стандартне відхилення. Прикладом перевірки таких гіпотез є з'ясування питання про те,змінюється чи не змінюється виробничий процес з часом. Прикладом оцінки параметрів є оцінка середнього значення статистичної змінної за дослідними даними. Для вивчення статистичної залежності використовують методи теорії кореляції. Загальні методи математичної статистики є основою теорії похибок. 

Математична статистика широко використовує методи теорії ймовірностей для вибудови і перевірки математичних моделей. Її методи розширюють можливості наукового передбачення і раціонального прийняття рішення багатьох задач, де суттєві параметри не можуть бути з'ясовані чи контрольовані з достатньою точністю.

Основні поняття математичної статистики

1. Статистичні дані — сукупність чисел, які дають кількіс­ну характеристику ознак певних об'єктів та явищ, що нас цікавлять.
2. Відібрану для спостереження сукупність об'єктів називають вибірковою сукупністю або вибіркою.
3. Кількість об'єктів сукупності називають об'ємом сукуп­ності.
4. Числа, що є значеннями ознак кожної групи, на які можна поділити вибірку, називають варіантами; послідовність ва­ріант називають варіаційним рядом.
5. Частоти — числа, які показують, скільки разів повторювалось кожне значення ознаки сукупності.
6. Відношення частоти до об'єму вибірки називають відносною частотою.

Зведення статистичних даних. Для обробки статистичних даних виконують їх зведення, тобто упорядковують, узагальнюють статистичні дані.

Способи зведення статистичних даних:
1)      складання статистичного ряду;
2)      складання статистичної таблиці розподілу вибірки;
3)      складання полігона частот;
4)      складання гістограм.

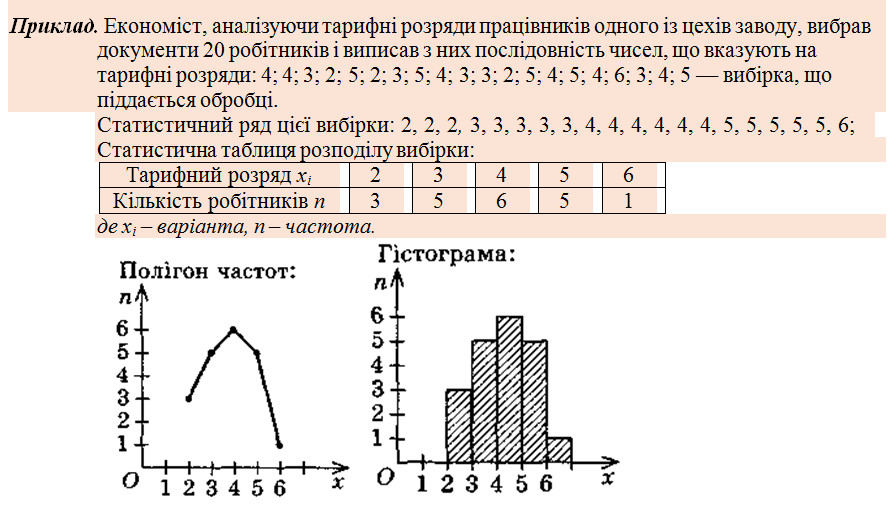
Центральні тенденції. Вибірки характеризуються центральними тенденціями: середнім значенням, модою і медіаною

В математиці середнє значення має різні визначення в залежності від контексту.

В теорії ймовірностей та статистиці середнє значення та математичне сподівання використовуються як синоніми для позначення мір центральної тенденції або розподілу ймовірностей, або випадкової змінної, що характеризується цим розподілом. Для набору даних для позначення центрального значення дискретного набору чисел, а саме, суми цих значень, поділеної на їхню кількість, також використовуються як синоніми терміни середнє арифметичне та математичне сподівання. Середнє арифметичне набору чисел x₁, x₂, …, x_n зазвичай позначають через , вимовляючи як «x із рискою». Якщо набір даних ґрунтувався на ряді спостережень, отриманих вибіркою зі статистичної сукупності, то середнє арифметичне називається вибірковим середнім (позначається через ), щоби відрізняти його від середнього значення сукупності (µ або µ_х).

Для скінченної сукупності середнє значення сукупності за певною властивостю дорівнює середньому арифметичному даної властивості за всіма членами цієї сукупності. Наприклад, середнє значення зросту для сукупності дорівнює сумі зростів кожної особи, діленої на загальну кількість осіб. Вибіркове середнє може відрізнятися від середнього сукупності, особливо для малих вибірок. Закон великих чисел каже, що чим більшим є розмір вибірки, тим правдоподібнішою є близькість вибіркового середнього до середнього сукупності.

За межами теорії ймовірностей та статистики широкий спектр інших значень «середнього» часто використовується в геометрії та математичному аналізі; нижче наведено приклади.

Контрольні запитання

1. Що таке математична статистика?
2. Що таке вибіркова сукупність?
3. Що таке статистичний ряд?
4. Що таке статистична таблиця?
5. Що таке варіанта; варіаційний ряд?
6. Що називають частотами?
7. Що називають відносною частотою?
8. Що таке полігон (частот)?
9. Що таке гістограма?
10. Cформулюйте формулу для обчислення простого середнього ариф­метичного. Наведіть приклади.
11. Сформулюйте формулу для обчислення зваженого середнього ариф­метичного. Наведіть приклади.
12. Що таке мода? Що показує мода? Наведіть приклади.
13. Що таке медіана? Наведіть приклад.